Having spent about three weeks on my first game concept I realised I had bitten off a little more than I could chew given my novice status in game design and development. That said which ever route I took there is a physics concept or mathematical gymnastics to perform and there was no getting away from it I was going to have to learn some stuff.
As you may also know I am currently working with the Corona SDK development framework and started looking at the excellent Flight Path sample template which can be viewed here. What I intend to do is write a mini series to document my learnings as well as hope this helps someone else in the future.
For those of you who aren't familiar with the concept of catmull splines (and don't worry I wasn't 72 hours ago), they can be described as splines which are a mathematical means of representing a curve, by specifying a series of points at intervals along the curve and defining a function that allows additional points within an interval to be calculated. There are various functions available to approximate a curve, but in this blog we will focus on a spline known as the catmull spline.
The points that define a spline are known as Control Points. One of the features of the catmull spline is that the specified curve will pass through all of the control points - this is not true of all types of splines.
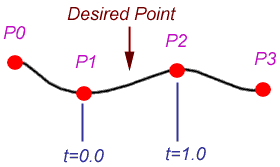
To calculate a point on the curve, two points on either side of the desired point are required, as shown on the left. The point is specified by a value t that signifies the portion of the distance between the two nearest control points.
Given the control points P0, P1, P2, and P3, and the value t, the location of the point can be calculated as (assuming uniform spacing of control points):
q(t) = 0.5 *( (2 * P1) +
(-P0 + P2) * t +
(2*P0 - 5*P1 + 4*P2 - P3) * t2 +
(-P0 + 3*P1- 3*P2 + P3) * t3)
Ermmmm, don't know about you but this is gibberish to me!
While a spline segment is defined using four control points, a spline may have any number of additional control points. This results in a continuous chain of segments, each defined by the two control points that form the endpoints of the segments, plus an additional control point on either side of the endpoints. Thus for a given segment with endpoints Pn and Pn+1, the segment would be calculated using [Pn-1, Pn, Pn+1, Pn+2].
Because a segment requires control points to the outside of the segment endpoints, the segments at the extreme ends of the spline cannot be calculated. Thus, for a spline with control points 1 through N, the minimum segment that can be formulated is P1<->P2, and the maximum segment is PN-3<->PN-2. Thus, to define S segments, S+3 control points are required.
Now what does that all mean to us Corona SDK developers using lua. Well, again, if you have followed my blogs you would know I have hailed the efforts of Matthew Pringle and his Corona Remote app to aid rapid testing. Those who have used it know of the plotting of accelerometer points. Matthew very kindly posted some code on the ansca website which helps put the gibberish above into context. The code is as follows:
display.setStatusBar( display.HiddenStatusBar )
-- New Points Table
points = {}
-- New Line
local line
-- Add Points - Generated Randomly To Draw Jagged Line Across Screen
for i = 1, 11 , 1 do
local xPoint = ( display.contentWidth / 10 ) * i - ( display.contentWidth / 10 )
local yPoint = math.random( 50 , 250 )
table.insert( points , 1 , { x = xPoint , y = yPoint } )
end
-- Draw Jagged Line
if ( #points > 2 ) then
line = display.newLine( points[1].x , points[1].y , points[2].x , points[2].y )
for i = 3 , #points , 1 do
line:append( points[i].x , points[i].y )
end
line:setColor( 155 , 155 , 155 )
line.width = 2
end
-- Catmull Spline Function
function drawCatmullSpline( p0 , p1 , p2 , p3 , steps )
local points = {}
for t = 0 , 1 , 1 / steps do
local xPoint = 0.5 * ( ( 2 * p1.x ) + ( p2.x - p0.x ) * t + ( 2 * p0.x - 5 * p1.x + 4 * p2.x - p3.x ) * t * t + ( 3 * p1.x - p0.x - 3 * p2.x + p3.x ) * t * t * t )
local yPoint = 0.5 * ( ( 2 * p1.y ) + ( p2.y - p0.y ) * t + ( 2 * p0.y - 5 * p1.y + 4 * p2.y - p3.y ) * t * t + ( 3 * p1.y - p0.y - 3 * p2.y + p3.y ) * t * t * t )
table.insert( points , { x = xPoint , y = yPoint } )
local dot = display.newCircle( xPoint , yPoint , 2 )
dot:setFillColor( 255 , 0 , 0 )
end
return points
end
-- Draw Curve Using Catmull Spline Function
if ( #points > 2 ) then
-- Steps Per Segment - The Higher The Number - The Smoother The Curve - The Longer It Takes To Calculate
local curveSteps = 5
-- First Segment
local firstSegement = drawCatmullSpline( points[1] , points[1] , points[2] , points[3] , curveSteps )
-- Draw First Segment
local curve = display.newLine( firstSegement[1].x , firstSegement[1].y , firstSegement[2].x , firstSegement[2].y )
for i = 3 , #firstSegement , 1 do
curve:append( firstSegement[i].x , firstSegement[i].y )
end
-- Segments Inbetween
for i = 2 , #points - 2 , 1 do
local middleSegment = drawCatmullSpline( points[i-1] , points[i] , points[i+1] , points[i+2] , curveSteps )
for i = 2 , #middleSegment , 1 do
curve:append( middleSegment[i].x , middleSegment[i].y )
end
end
-- Last Segment
local lastSegment = drawCatmullSpline( points[#points-2] , points[#points-1] , points[#points] , points[#points] , curveSteps )
for i = 2 , #lastSegment , 1 do
curve:append( lastSegment[i].x , lastSegment[i].y )
end
curve:setColor( 0 , 0 , 255 )
curve.width = 2
end
The results of which put the equation above into something a little more tangible:
Wow that was a lot to take in but hopefully putting it all in one place has helped a little. As I mentioned I am a newbie on this so if anyone reading this thinks what the hell is he talking about this is completely wrong I am more than happy to be corrected just leave a comment.
The next in the series I will look into something more akin to a game and applying the Corona SDK template for novices. Stay tuned ...







0 comments:
Post a Comment